二叉数：

  • 二叉树递归遍历

  • 二叉树非递归遍历

  • 宽度优先遍历

  • 搜索二叉树

  • 完全二叉树

  • 满二叉树

  • 平衡二叉树

// 二叉树节点
class Node<V> {
    V value;
    Node left;
    Node right;
}

头节点：也叫根节点，二叉树最顶端的节点（无无父结点）

叶节点：左右子节点都为null

子树：以任意一节点为根，其衍生下可以直接相连或经过节点相连的全部节点组成的树

二叉树遍历：

使用递归方式实现：

// 二叉树每个节点遍历时都有三次访问
public static void f(Node head) {
    //1:start
    if (head == null) {
        return null;
    }
    ...
    // 1:end
    f(head.left);
    // 2:start
    ...
    // 2:end
    f(head.right);
    // 3:start
    ...
    // 3:end
}

*先序，中序，后序遍历即是在第一次，第二次，第三次访问节点时做反应

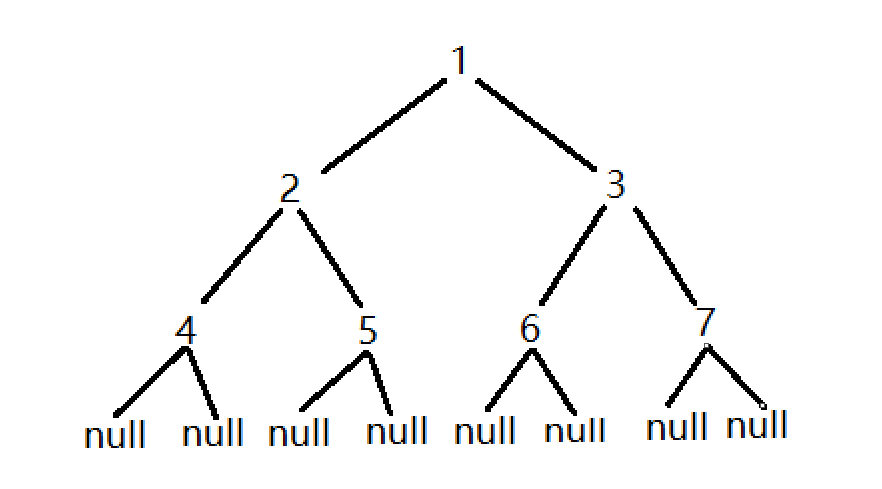
image-20220812185607833

遍历打印（每次访问打印一次value）：

1 2 4 4 4 2 5 5 5 2 1 3 6 6 6 3 7 7 7 3 1

先序访问顺序（对每颗子树 头左右）：

1 2 4 5 3 6 7

中序访问顺序（对每颗子树 左头右）：

4 2 5 1 6 3 7

后序访问顺序（对每颗子树 左右头）：

4 5 2 6 7 3 1

使用非递归方式实现二叉树：

先序遍历：
  1. 创建一个栈（Stack）对象，将头节点压入栈列
  2. 弹出栈顶节点 Car
  3. 打印处理 Car
  4. 先压入右节点，再压入左节点（有就压）
  5. 返回第二步，直至栈空
//代码实现
public static void preOrder(Node head) {
    if(head != null){
        Stack<Node> stack = new Stack<Node>();
        stack.push(head);
        while(!stack.isEmpty()) {
            head = stack.pop();
            System.out.println(head.value());
            if(head.right != null) {
                stack.push(head.right);
            }
            if(head.left != null) {
                stack.push(head.left);        
            }
        }
    }
}
中序遍历：
  1. 创建一个栈，将数的最左边界依次压入
  2. 弹出打印栈顶元素，若栈顶存在右子树，将右子树的最左边界依次压入
  3. 循环2，直至栈空
public static void (Node head) {
    if(head != null) {
        Stack<Node> stack = new Stack<>();
        while(!stack.isEmpty() || head != null) {
            if(head != null) {
                stack.push(head);
                head = head.left;
            }else {
            head = stack.pop();
            System.out.println(head.value());   
            head = head.right;
            }
        }
    }
}
后序遍历：
  1. 创建两个栈（存储栈和收集栈）
  2. 弹出存储栈头节点，压入收集栈
  3. 将2中弹出的节点，以先压左节点再压右节点的顺序压入存储栈
  4. 返回2，直到存储栈为空
  5. 依次打印收集栈顺序
public static void posOrder(Node head) {
    if(head != null) {
        Stack<Node> st1 = new Stack<>();
        Stacj<Node> st2 = new Stack<>();
        st1.push(head);
        while(!st1.isEmpty()){
            head = st1.pop();
            st2.push(head);
            if(head.left != null){
                st1.push(head.left);
            }
            if(head.right != null) {
                st1.push(head.right);
            }
        }
        while(!st2.isEmpty()){
            System.out.println(st2.pop().value);
        }
    }
}

实现二叉树的宽度优先遍历：

使用队列：
  1. 创建一个队列（Queue）对象，将头节点放入队列
  2. 弹出打印队列首个对象，将其左子树先放入队列，再放其右子树（如果有）
  3. 循环2，直到队列为空
public static void widthOrder(Node head) {
    if(head == null) return;
    Queue<Node> queue = new LinkedList<>();
    queue.add(head);
    while(!queue.isEmpty()) {
        head = queue.poll();
        System.out.println(head.value);
        if(head.left != null) {
            queue.add(head.left);
        }
        if(head.right != null) {
            queue.add(head.right);
        }
    }
}
算法题：求一个二叉树的最大宽度？
  1. 创建一个队列（Queue）对象，将头节点放入队列
  2. 创建一个hashMap对象，用于记录节点与当前所在深度，将<head, 1>记录
  3. 创建初始深度（int）设为1，初始节点数（int）设为0，初始最大值（int）设为Integer.MIN_VALUE;
  4. 弹出队列首个对象，并根据HashMap判断该节点是否是当前深度的节点，是：节点数++，否：最大值=max（max，节点数），深度++，节点数设为1
  5. 将其左子树先放入队列，hashMap放入<head.left，深度+1>；再放其右子树，hashMap放入<head.right，深度+1>（如果有）
  6. 循环2-5，直到队列为空
  7. 调用Max函数计算最后一行节点个数和最大节点的比较
public static void getMaxWidth(Node head) {
    if(head == null) return;
    Queue<Node> queue = new LinkedList<>();
    queue.add(head);
    HashMap<Node,Integer> levelMap = new HashMap<>();
    levelMap.put(head,1);
    int curlevel = 1;		//当前层数
    int curNodeNum = 0;		//当前节点数
    int max = Integer.MIN_VALUE;	//最大节点值
    while(!queue.isEmpty()) {
        head = queue.poll();
        int levelNode = levelMap.get(head);
        if(levelNode == curlevel) {		//判断是否变层
            cerNodeNum ++;				//未变层，节点数++
        }else {
            max = Math.max(max, curNodeNum);	//下一层，结算上一层的max，重置当前节点数
            curLevel ++;
            curNodeNum = 1;
        }
        if(head.left != null) {
            queue.add(head.left);
            levelMap.put(head.left,curlevel+1)		//记录左子树以及其对应层，用于后续判断
        }
        if(head.right != null) {
            queue.add(head.right);
            levelMap.put(head.right,curlevel+1)		//记录右子树以及其对应层，用于后续判断
        }
    }
    max = Math(max, curNodeNum);
}
*不使用哈希表完成上述题目：

使用两个Node变量替代哈希表（当前层最后的节点，下一层最后的节点）

将head赋予当前层最后节点，在每次新添左右节点时，分别更新下一层最后节点为左右节点

每次队列弹出都检查是否是当前层最后节点，是：更新最大值，拷贝下一层最后节点至当前层最后节点，层数++；否：节点数++

二叉树深度优先遍历：先序遍历

搜索二叉树：

对于每一个子树，都满足其左树值比根节点值小，右树值比根节点大（一般不存在重复值）

如何判断是否是搜索二叉树：中序遍历为升序
public static int prevalue = Integer.MIN_VALUE;

public static boolean isBSt(Node head) {
    if(head == null) return true;
    boolean isLeftBst = isBST(head.left);	//左子树是否为搜索二叉树
    if(!isLeftBst) return false;
    if(head.value <= preValue) {	//升序判断，动态检查
        return false;
    }else {
        preValue = head.value;
    }
    return isBST(head.right);	//左子树是搜索二叉树，右子树是否为搜索二叉树
}

非遍历判断同理

总结返回信息：

对于左子树：1.左树应是搜索二叉树 2.获取左数的最大值（用于与根比较）

对于右子树：1.右树应是搜索二叉树 2.获取右数的最小值（用于与根比较）

统一左右子树返回信息：是否是搜索二叉树，最小值，最大值

判断是否为搜索二叉树：
public static boolean checkBST(Node head) {
    return process(head).isBST;
}

//返回类型
public static class ReturnType {
    public boolean isBST;
    public int min;
    public int max;
    
    public ReturnData(boolean isb, int min, int max){
        this.isBST = isb;
        this.min = min;
        this.max = max;
    }
}

public static ReturnType process(Node x) {
    if(x == null) return null;
    ReturnType leftData = process(x.left);
    ReturnType rightData = process(x.right);

    //获得整个子树的最大最小值
    int min = x.value;
    int max = x.value;
    if(leftData != null) {
        min = Math.min(min,leftData.min);
        max = Math.max(max,leftData.max);
    }
    if(rightData != null) {
        min = Math.min(min,rightData.min);
        max = Math.max(max,rightData.max);
    }
       
    boolean isBST = true;
    if(leftData != null && (!leftData.isBST || leftData.max >= x.value) {
        isBST = false;
    }
    if(rightData != null && (!rightData.isBST || x.value >= rightData.min) {
        isBST = false;
    }
   
    return new ReturnType(isBST,min,max);
}

完全二叉树：

所有节点依次按从左往右依次放入的二叉树属于完全二叉树

  1. 任意一节点有右孩子无左孩子 → 不是完全二叉树
  2. 宽度优先遍历且在不违反1前提下，出现首个左右孩子不双全时，之后的节点都应该是叶子节点
public static boolean isCBT(Node head) {
    if(head == null) return true;
    //是否遇到过左右孩子不双全的判断
    boolean leaf = false;
    Node l = null;
    Node r = null;
    Queue<Node> queue = new LinkedList<>();
    queue.add(head);
    while(!queue.isEmpty()) {
        head = queue.poll();
        l = head.left;
        r = head.right;
        if((leaf && (l!=null || r!=null))	//条件2
          ||
           (l == null && r == null)	//条件1
          ){
            return false;
        }
        if(l != null) {
            queue.add(l);
        }
        if(r != null) {
            queue.add(r);
        }
        if(l == null || r == null) {
            //leaf 为不可逆改变
            leaf = true;
        }   
    }
    return true;
}

满二叉树：

子节点要么都有，要么都没有，不存在只存在一边节点的二叉树

判断是否为满二叉树：
public static boolean isFBT(Node head) {
    if(head == null) {
        return true;
    }
    info data = process(head);
    return data.nodes == ((1<<data.height) - 1);
}

//返回信息
public static class Info {
    public int height;			//高度
    public int nodes;			//节点数
    
    public Info(int hei, int nod) {
        this.height = hei;
        this.nodes = nod;
    }
}
//过程函数，返回类型为ReturnType
public static Info process(Node x) {
    if(x == null) {
        return new Info(0, 0);
    }
    
    Info leftData = process(x.left);
    Info rightData = process(x.right);
    
    int height = Math.max(leftData.height,rightData.height)+1;
    int nodes = leftData.nodes + rightData.nodes + 1;
    
    return new Info(height, nodes);
}

平衡二叉树：

对于任意一颗子树，其左树高度和右树高度差不少过1

  1. 节点左树是平衡二叉树
  2. 节点右树是平衡二叉树
  3. |节点左树高度 - 节点右数高度| <= 1

以上条件对每个节点都成立，这个树就是平衡二叉树，否则不是

总结返回信息：

对于左树，我们希望知道：1.左树是否是平衡二叉树 2.左树高度

对于右数，我们希望知道：1.右树是否是平衡二叉树 2.右数高度

左右树需要的信息一致；

判断是否为平衡二叉树：
//返回值的变动，调用其他方法返回
public static boolean isBT(Node head) {
    return process(head).isBalanced;
}

//返回信息
public static class ReturnType {
    public boolean isBalanced;	//是否是平衡二叉树
    public int height;			//高度
    
    public ReturnType(boolean isB, int hei) {
        this.isBalanced = isB;
        this.height = hei;
    }
}
//过程函数，返回类型为ReturnType
public static ReturnType process(Node x) {
    if(x == null) {
        return new ReturnType(true, 0);
    }
    
    ReturnType leftData = process(x.left);
    ReturnType rightData = process(x.right);
    
    int height = Math.max(leftData.height,rightData.height)+1;
    boolean isBalance = leftData.isBalanced && rightData.isBalanced
                        && Math.abs(leftData.height - rightData.height) < 2;
    
    return new ReturnType(isBalance, height);
}